differentiable_dsls

· atharvas's blog

Request: This is work in progress and the blogging equivalent of rubber duck debugging. Please please please don't share this forward.

Overview #

I saw a survey on HN a couple of days ago about what we know about the generalizability of deep neural networks. One of the sections in this work talked about how 'vanilla' forms of regularization don't seem to aid the generalizability of DNNs. I really liked the discussion around this and wanted to pen down some ideas from my area of research, neurosymbolic learning, that hint at how structured regularization can help DNN generalization. Specifically, in part one of me yelling into the void, I wanted to yell talk about how differentiable domain specific languages (DSLs) seem to be a neat way of regularizing DNNs that has worked well for me.

What do I mean by "Structured Regularization" #

DNNs operate on Bayes theorem. Here it is restated for the billionth time:

1P(model_weights|data) . P(data) = (P(data|model_weights) . P(model_weights) )

If we massage this enough, we get:

1P(model_weights|data) ~= P(data|model_weights) . P(model_weights)
2│                           │                       │
3│                           │                       └── prior
4│                           └── likelihood
5└── posterior

I'll define "regularization" as further massaging the prior to obey a certain property. L1 loss is a form of "unstructured regularization"; it makes no assumptions about the data in enforcing its constraints. Consecutively, "structured regularization" is a form of regularization that enforces its constraints by using some prior knowledge gathered either from the dataset or from experts. This structured regularization exists on a gradient on how expressive the constraints are/

1<high ----------- somewhere in the middle ----------- low>
2│                   │                                   │
3│                   │                                   └── propositional logic regularizer := eg: ImageNet image normalization
4│                   └── weak supervised regularizer := eg: we bias the model towards something an expert told us
5└── neurosymbolic regularizer := eg: differentiable dsl

Differentiable DSLs #

Every programming language has a syntax and a semantics. We use CFGs to discuss the syntax of a language and Proof Trees to discuss the semantics of the language (This is all coming out of CS421). How would we make a programming language that can "interface" with a neural network? Well the syntax is kind of dependent on the task at hand and the output of the neural network -- if I have a neural network that looks at a traffic camera and gives me bounding boxes like this: 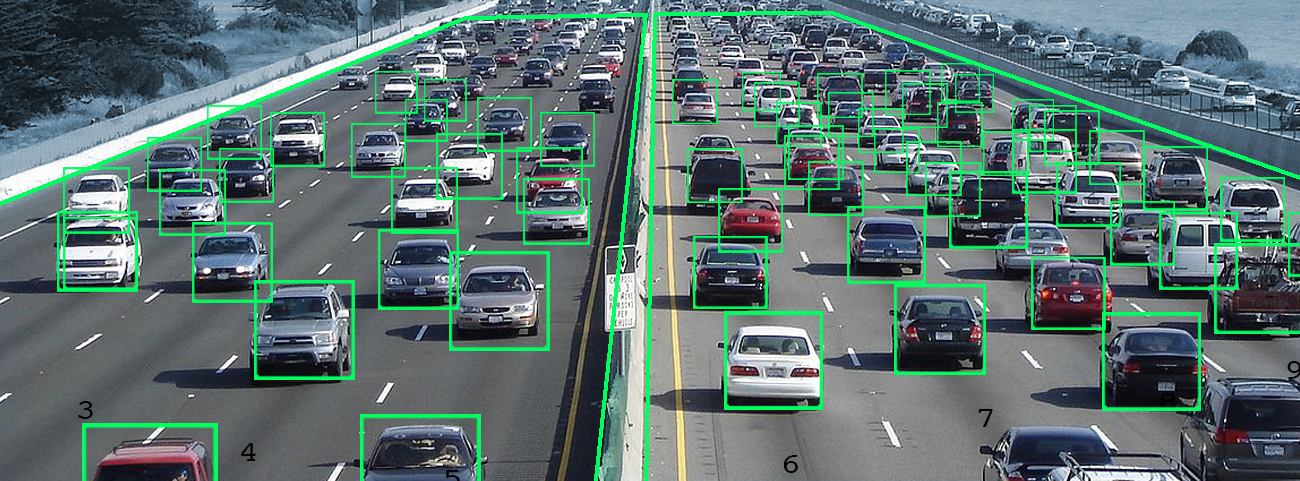traffic_camera_dataset I can define a simple grammar over the x-y coordinates of the centroid of the bounding boxes:

Expr := select_centroid_x
    | select_centroid_y
    | Add(Expr, Expr)
    | Multiply(Expr, Expr)
    | Map(\lambda x : Expr(x), xs)
    ...

This grammar potentially allows me to reason about various properties of the cars. For example: velocity can be defined by Divide(Subtract(head(sequences_of_ys), head(reversed(sequences_of_ys)), len(sequences_of_ys) * FPS) (aka: calculate the displacement of the y coordinate and divide by the number of frames times the frames per second). Now, we can add a constraint abs(velocity) <= 300 mph that is general enough to capture the behavior of all cars (other than those driven by certain characters on the Autobahn). In general, we can use a lot of cool techniques from Program Verification and Program Synthesis to reason about properties in certain domains. So our pipeline currently looks like this:

1(Sequence of Images) --[Object Detector]--> (Sequence of Points) --[Program]--> (Valid Inference?)

However, to train the object detector, we need our program to be differentiable. This step requires us to use another programming languages technique called lifting. The essential idea is the same as operator overloading. Operationally, we construct our semantics to make sure that each of the expression is backpropogatable. Basically,

1PyTorchExpr := (
2    lambda arr: arr[0], # select_centroid_x
3    lambda arr: arr[1], # select_centroid_y
4    lambda arr_of_arr: arr_of_arr.sum(axis=0), # Add(Expr, Expr),
5    lambda arr_of_arr: arr_of_arr.prod(axis=0), # Multiply(Expr, Expr),
6    lambda arr_of_arr: arr_of_arr.map(PyTorchExpr) , # Map(\lambda x : Expr(x), xs)

I'm hand waving a lot of PyTorch details here but I hope I've convinced you that it's not hard to engineer differentiable relaxations of pytorch functions (For a more operational version of this checkout this). Formulating our semantics by lifting our DSL functions to continuous relaxations in PyTorch allows us to backpropogate through any valid program!

1(Sequence of Images) --[Object Detector]--> (Sequence of Points) --[Program]--> (Valid Inference?)
2    └───◄───────────────────(backward)──────────◄──────────────────(backward)──────────◄───┘

And this, in my mind, is a very very very primitive way of operationalizing structured regularization for a DNN.

What's the catch? #

No free lunch, amirite? The biggest issue with this approach is that we are essentially synthesizing/verifying a program with gradient descent. Programs are inherently non-smooth. If we aren't careful with the primitive functions we're using, we might destroy the smoothness of the optimization landscape and learn nothing (the training curve looks like a zig-zag line that goes anywhere but down). However, to push back a little on this: this is all conditioned on if we aren't careful with our problem formulation. Check out Daniel Selsam's work on NeuroSAT and NeuroCore for a neural pipeline for program verification that kinda works (dselsam.github.io)!

Okay, now show me results. #

@TODO. Stay tuned! Till then check out some of the cool papers that I was thinking about while writing this down:

Lemme know if you have any thoughts/opinions/concerns about this! (atharva.sehgal@gmail.com)